Características del motor

Video resumen Características del motor

El motor térmico del automóvil transforma la energía de la combustión en movimiento circular mediante el pistón, biela y cigüeñal.

Las dimensiones y otras particularidades de los componentes del motor nos dan sus características, de las que depende en principio el rendimiento que se va a obtener.

Vamos a ver en este artículo las características del motor más frecuentes que se incluyen en las fichas técnicas.

Presentación de las características del motor

Se ve en las imágenes un motor con árbol de levas en culata o cabeza funcionando, de frente y de lado con cuatro cilindros en línea.

En esta animación se presentan las características del motor que se verán después con detalle:

• Diámetro del cilindro
• Carrera del pistón
• Cilindrada, unitaria y total
• Relación de compresión
• Velocidad lineal del pistón

De estas características unas son dimensionales, otras de relación entre varias y otras resultado de las RPM del motor.

Empezamos con el diámetro y la carrera.

Diámetro y carrera

En el motor de cuatro cilindros en línea identificamos el diámetro y la carrera:

• Diámetro D (morado); es el del cilindro y se mide en milímetro (mm). Lo vemos en detalle separado del motor
• Carrera C (verde); es el recorrido vertical del pistón en el cilindro y se mide igualmente en mm, se resalta en el detalle a la derecha del motor
• A continuación se representa el diámetro en los cuatro cilindros abarcando solamente el recorrido del pistón
• La carrera se refleja en los cuatro cilindros resaltando el recorrido del pistón en su interior

El diámetro y la carrera determinan el tamaño del cilindro.

Cilindrada unitaria y total

Esta animación nos va a explicar la cilindrada unitaria y total de un motor, en este caso de cuatro cilindros:

• Cilindrada; se ve en uno de los cilindros del motor y se resalta en el detalle de la derecha, es el volumen del cilindro recorrido por el pistón (amarillo)
• Es la cilindrad unitaria C_U, es decir solamente de uno de los cilindros
• Cilindrada total C_T; se ve en los cuatro cilindros del motor y se representa en detalle
• La fórmula que da la cilindrada total es C_T = C_{U x} Número de cilindros, en este caso son 4

La cilindrada del motor se mide en centímetros cúbicos (cc) o litros (l).

Si el motor tiene un cilindro, la cilindrada unitaria es también la total.

Cálculo de la cilindrada de un motor

La cilindrada total del motor se obtiene multiplicando la cilindrada unitaria por el número de cilindros, pero antes se ha de calcular ésta, la animación siguiente nos ayuda a verlo con las fórmulas:

• Fórmula del volumen de un cilindro V_C:

• • V_C en cc
  • Pi; 3,1416….
  • R; radio del cilindro (en cm para obtener el volumen en cc)
  • H; altura del cilindro (en cm para obtener el volumen en cc)
• Fórmula del volumen del cilindro de un motor, cilindrada unitaria C_U:

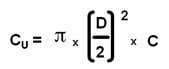
• • C_U en cc
  • Pi; 3,1416….
  • D diámetro (en cm), se divide por 2 para obtener el radio
  • C carrera (en cm)
• Fórmula del la cilindrada del motor C_T con varios cilindros:

• A continuación proponemos tres aplicaciones de las fórmulas sobre automóviles reales
• Audi Quattro:
  • 5 cilindros en línea
  • Diámetro (D) 79,5 mm (7,95 cm)
  • Carrera (C) 86,4 mm (8,64 cm)
  • Aplicando la fórmula de C_U da 428,8 cc
  • La CT se obtiene multiplicando por 5; 2.144 cc o 2,1 l (litros)
• Saab 92:
  • 2 cilindros en línea
  • Diámetro (D) 80 mm (8,0 cm)
  • Carrera (C) 76 mm (7,6 cm)
  • Aplicando la fórmula de C_U da 382 cc
  • La CT se obtiene multiplicando por 2; 764 cc o 0,76 (litros)
• Lamborghini Miura:
  • 12 cilindros en V
  • Diámetro (D) 82 mm (8,2 cm)
  • Carrera (C) 62 mm (6,2 cm)
  • Aplicando la fórmula de C_U da 327,4 cc
  • La CT se obtiene multiplicando por 12; 3.929 cc o 3,9 l (litros)

Para una cilindrada total, cuanto menor sea la cilindrada unitaria genéricamente menos vibraciones producirá el funcionamiento del motor.

En un automóvil medio se considera que el valor óptimo entre coste y resultados es de 500 cc.

Otra forma de decirlo es que en cuantos más cilindros se divida la cilindrada total mejor para la suavidad de funcionamiento, pero supone más rozamientos internos y costes.

Relación de compresión

Este dato tiene importancia en el rendimiento del motor, sobre todo antes de la sobrealimentación.

La relación de compresión R_C se explica con la siguiente animación:

• Volumen de admisión V_A; es el volumen que hay sobre el pistón cuando está en la parte inferior (punto muerto inferior PMI). Es la cilindrada unitaria más el volumen de la cámara de combustión. Se ve en el motor y en detalle separado (amarillo)
• Volumen de compresión V_C; es el volumen sobre el pistón estando en su recorrido más alto en el motor (punto muerto superior PMS). Es el volumen de la cámara de combustión. Se resalta sobre el motor y en detalle separado (rojo)
• Relación de compresión R_C; esta es su fórmula:

• Tomando por ejemplo que la RC de un motor es 9,5 se representa así; 9,5 : 1, indicando el número de veces que el volumen de compresión V_C está contenido en el de admisión V_A como referencia 1

Antes de la sobrealimentación en el motor de gasolina a mayor relación de compresión mejor rendimiento, pero con gasolina de mayor índice de octano.

En los motores diésel la relación de compresión determina la capacidad de iniciar la combustión del gasóleo.

Para calcular la relación de compresión se ha de tener en cuenta la forma de la cabeza del pistón, que puede aumentar o disminuir el volumen de la cámara de combustión.

Una forma de calcular la R_C es medir los volúmenes afectados experimentalmente.

Motores con diámetro (D), carrera (C) y R_C diferentes con la misma cilindrada

Se ven las representaciones de dos motores OHC con cuatro cilindros en línea y la misma cilindrada, obtenida de distinta forma:

• A la izquierda el motor de un Mazda 6 G 2.0 Skyactiv (2015)
  • Diámetro D; 83,5 mm
  • Carrera C; 91,5 mm
  • Cilindrada, 1.998 cc
  • R_C; 14,0 : 1
• A la derecha el motor de un Mazda MX5 (2015)
  • Diámetro D; 87,5 mm
  • Carrera C; 83,1 mm
  • Cilindrada, 1.999 cc
  • R_C; 10,8 : 1

• El motor del Mazda 6 tiene menos diámetro y más carrera que el del MX5 para obtener la misma cilindrada
• La relación de compresión R_C es muy diferente, 14 en le Mazda 6 y 10,8 en el MX5.

Como curiosidad técnica, la elevada relación de compresión del motor del Mazda 6 (14:1) es por tener inyección directa de gasolina y tratar de funcionar próximo a la combustión HCCI (llenado, compresión y combustión homogéneos).

Si estos temas te interesan tienes más información en estos artículos del blog; “Inyección indirecta y directa en el motor de gasolina” en la sección “Actualidad”, y el artículo “Combustión HCCI” en la sección “Tecnologías limpias”.

Velocidad lineal del pistón VP y relación con el par y la potencia

Los pistones se desplazan por el interior de los cilindros a velocidades muy rápidas.

Se denomina velocidad lineal del pistón V_P a este dato y se da en metros por segundo (m/s).

En la animación siguiente seguimos con los dos motores de Mazda que ya conocemos, pues tienen diferentes valores de carrera C, que influye en la velocidad de desplazamiento de los pistones, y son útiles para las explicaciones:

• De los datos que vemos en la animación nos interesan los dos de la carrera; 83,1 mm para el motor de la izquierda (Mazda 6) y 91,2 mm para el de la derecha (Mazda MX5)
• Aparece la fórmula de la velocidad lineal del pistón V_P:

• RPM; revoluciones por minuto
• C carrera en milímetros
• El denominador, 3 _x 10⁴, es para obtener el resultado en metros por segundo m/s
• Para que los resultados sean didácticamente más comparativos tomamos como referencia 5.000 RPM en ambos motores y aplicamos la fórmula a cada uno de ellos en función de los valores de sus respectivas carreras:
  • V_P con 83,1 de carrera = 13,8 m/s (motor de la izquierda)
  • V_P con 91,2 de carrera = 15,2 m/s (motor de la derecha)

• Comparación de par y potencia:
  • Junto al motor de la izquierda aparece en detalle el cilindro con más diámetro y menos carrera, y junto al motor de la derecha el detalle del cilindro con menos diámetro y más carrera
  • En ambos motores están los datos de sus características, de los que se ha utilizado el correspondiente a las respectivas carreras para el cálculo de la velocidad del pistón V_P
  • En los detalles de los cilindros se resalta la distancia entre el apoyo del cigüeñal en el bloque y en la biela, que es la mitad de la carrera C/2
  • Esta distancia es mayor, evidentemente, en el motor con más carrera
  • A continuación se observa como la fuerza de la explosión llega desde el pistón al apoyo de la biela en el cigüeñal F_E, esta fuerza consideramos que es igual en los dos motores
  • El par motor es el resultado de multiplicar la fuerza de la explosión aplicada en el apoyo biela – cigüeñal F_E, por la distancia entre dos puntos de giro del cigüeñal C/2; Par = F_{E x} C/2
  • En el motor con menos carrera (izquierda) el valor del par es menor que en el motor de más carrera (derecha)
  • La potencia se obtiene multiplicando el par por las RPM; = Par _x RPM
  • El motor con menos carrera (izquierda) puede girar a más RPM pues la velocidad del pistón es menor, lo que le permite lograr más potencia que en el motor con más carrera
  • Se deduce de todo esto que con más carrera se favorece el par, es decir la respuesta del motor a bajas y medias RPM, pero la potencia no será elevada
  • Con menos carrera se obtiene más potencia, pero la respuesta a bajas medias RPM es menos efectiva

En principio, cuanto mayor sea la velocidad del pistón más desgastes habrá en su rozamiento con el cilindro.

Depende también de otros factores como el peso, altura del pistón, calidades de los materiales, etc.

Se considera que en un automóvil de calle un valor a no sobrepasar en régimen de crucero es 15 m/s.

Este dato, con la masificación de la sobrealimentación, habría que reducirlo, pues los esfuerzos sobre el pistón a las mismas RPM que en un motor atmosférico son bastante más elevados y en consecuencia los rozamientos.

De hecho con la sobrealimentación se pueden lograr valores de par y potencia casi a la carta según las necesidades del motor en el automóvil que se monta.

Resumen de las características del motor

Con la animación siguiente damos un repaso al contenido de este artículo con tres coches que hemos utilizado y de los que incluimos todos los datos que hemos explicado:

Lamborghini Miura:

• Con su reducida carrera C de 62 mm la velocidad del pistón V_P, 10,3 m/s es la menor a 5.000 RPM
• Pero si se calcula al régimen de potencia máxima 7.000 RPM llega a 14,5 m/s, que no es excesiva para un automóvil deportivo de muy altas prestaciones
• Se busca potencia por RPM dando por hecho menos respuesta proporcional a bajas RPM

Saab 92:

• La carrera C de 76 mm es un valor medio de los tres coches, la velocidad del pistón V_P a 5.000 RPM es 12,6 m/s, lógicamente es también un valor medio
• El régimen de potencia máxima es 3.800 RPM y la correspondiente velocidad del pistón V_P es 9,6 m/s, muy conservadora
• Este motor es de 2 tiempos, si te interesa conocer más sobre este ciclo puede verlo en el artículo dedicado a este coche

Audi Quattro:

• La carrera C de 86,4 mm es la mayor de los tres lo que implica la velocidad de pistón V_P más elevada a 5.000 RPM, 14,4 m/s
• El régimen de potencia máxima es 6.700 RPM y supone una velocidad del pistón V_P de 19,3 m/s bastante elevada y más en un motor con turbocompresor
• Se trata de un automóvil deportivo muy prestacional, base para preparaciones destinadas a competición

Como se comentó antes, con la incorporación de la sobrealimentación en prácticamente todos los motores, se pueden lograr respuestas bastantes lineales al acelerador, lo que permite desarrollos de transmisión más largos con claros beneficios en consumo y contaminación.

Artículos relacionados

• 1.6.1 Motor de gasolina (I)
• 1.6.2. Motor de gaolina (II)
• 1.8.1. Par y potencia (I)
• Lamborghini Miura (P400)
• Saab 92 a 96
• Audi Quattro

Otros enlaces

• Características del motor
• Imagen Determinación de la cilindrada

Vídeos de interés